Warmly Welcome Dr. Lucian Sfîcă to the Editorial Board of JASR
2024-06-20
Coordinates over Complex Terrain in Atmospheric Model
Authors
-
Wen-Yih Sun
Department of Earth, Atmospheric and Planetary Sciences, Purdue University, W. Lafayette, IN, 47907, USA;Department of Atmospheric Sciences, National Central University, Chung-Li, Taoyuan, 320, Taiwan, China;Institute for Space-Earth Environmental Research, Nagoya University, Nagoya, 464-8601, Japan
DOI:
https://doi.org/10.30564/jasr.v4i1.2704Abstract
In the terrain following coordinate, Gal-Chen and Somerville and other proposed a vertical coordinate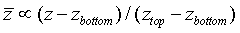 
and constant spatial intervals of 
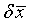and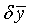 
along the other directions. Because the variation of 
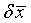and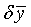 
was ignored, their coordinate does not really follow the terrain. It fails to reproduce the divergence and curl over a complex terrain. Aligning the coordinate with real terrain, the divergence and curl we obtained from the curvilinear coordinate are consistent with the Cartesian coordinate. With a modification, the simulated total mass, energy, and momentum from the Navier-Stokes equations are conserved and in agreement with those calculated from Cartesian coordinate.
Keywords:
Navier-Stokes equations; Cartesian; Curvilinear; Covariant; Contravariant; Terrain followingReferences
[1] Gar-Chen, T., R. C. J. Somerville. Numerical solution of the Navier-Stokes equations with topography. J. Comput. Phys., 1975, 17: 276-309.
[2] Kasahara, A.. Various Vertical Coordinate Systems Used for Numerical Weather Prediction., Mon. Wea. Rev., 1974, 102(7): 509- 522.
[3] Sun, W. Y., J. D. Chern. Diurnal variation of lee-vortexes in Taiwan and surrounding area. J. Atmos. Sci., 1993, 50: 3404-3430.
[4] Pacanowski, R. C. MOM 2 Documentation User’s Guide and Reference Manual version 1.0. GFDL Ocean Technical Report #3. 233pp. GFDL, NOAA, 1995.
[5] Saito K, K. T. Kato, H. Eito, C. Muroi. Documentation of the Meteorological Research Institute/Numerical Prediction Division Unified Nonhydrostatic Model. MRI Report, 2001, 42: 133.
[6] Staniforth A., W. White, N. Wood, J. Thuburn, M. Zerroukat, E. Corderro. Unified Model Documentation Paper. Joy of U.M. 6.0- Model Formulation. Dynamics Research Numerical Weather Prediction. Met Office, Devan, United Kingdom, 2004, 15.
[7] Tsuboki K., A. Sakakibara. Numerical Prediction of High-Impact Weather Systems, HYARC, Nagoya, 2007: 273.
[8] Skamarock, W. C., J. B. Klemp, J. Dudhia, D. O. Gill, D. M. Barker, M. G. Duda, X.-Y. Huang, W. Wang, J. G. Powers. A Description of Advanced Research WRF Version 3. NCAR/TN- 475+STR, 2008: 113pp
[9] Lin, M-Y, W. Y. Sun, M-D. Chiou, C-Y. Chen, H.-Y. Cheng, C.-H. Chen:. Development and evaluation of a storm surge warning system in Taiwan. Ocean Dynamics, 2018. DOI: https://doi.org/10.1007/s10236-018-1179-z
[10] Sun, W.Y., O. M. Sun. Revisiting the parcel method and CAPE, Dynamics of Atmospheres and Oceans, , 2019, 86: 134-152.
[11] Kapitza, H., D. P. Eppel. The non-hydrostatic mesoscale GESIMA. Part I: Dynamical equations and tests. Beitr. Phys. Atmosph., 1992, 65: 129-145.
[12] Pielke, Sr R. A. Mesoscale Meteorological Modeling. 2nd Ed. Academic Press, USA, 2002: 676.
[13] Pielke, R. A., W. R. cotton, R. L. Walko, C. J. Tremback, W. A. Lyons, L. D. Grasso, M. E. Nicholls, M. D. Moran, D. A. Wesley, T. J. Lee, J. H. Copeland. A comprehensive meteorological modeling system-RAMS. Meteor. Atmos. Phys., 1992, 49: 69-91.
[14] Sun, W. Y, O. M. Sun, K. Tsuboki. A Modified Atmospheric Nonhydrostatic Model on Low Aspect Ratio Grids-Part II. Tellus A 2013, 65: 19681 DOI: http://dx.doi.org/10.3402/tellusa.v65i0.19681
[15] Kusse, B. R., E. Westwig. Mathematical Physics, 2nd Ed. Wiley-VCH, Weinheim, Germany, 2006: 699.
[16] Kajishima, T., K. Taira. Computational Fluid Dynamics, Spring. Switzerland, , 2017: 358.
[17] Yang, H. Q., A. J. Przekwas. General strong conservation formulation of Navier-Stokes equations in nonorthogonal curvilinear coordinates, AIAA Journal, 1994, 32(5): 936-941.
[18] Wikipedia, Curvilinear coordinates: https://en.wikipedia.org/wiki/Curvilinear_coordinates
[19] Bellmann, R., 1997: Introduction to Matrix Analysis. ISBN: 0-89871-399-4 https://books.google.com/book?id=QVCflvTPYE8C).SIAM
[20] Hsu, W.-R., W. Y. Sun. A time-split, forward-backward numerical model for solving a nonhydrostatic and compressible system of equations. Tellus, 2001, 53A: 279-299.
[21] Chen, S. H., W. Y. Sun. The applications of the multigrid method and a flexible hybrid coordinate in a nonhydrostatic model. Mon. Wea. Rev., 2001, 129: 2660- 2676.
[22] MacCall, B. T. 2006: Application of Reynolds’ Stress Closure to the Stable Boundary Layer. Ph.D. Thesis, Dept. of Earth and Atmospheric Sciences, Purdue Univ., W. Lafayette, IN 47907.
[23] Sun, W. Y., K. S. Yeh. A general semi-Lagrangian advection scheme employing forward trajectories. J. R. Meteorol. Soc., , 1997, 123: 2463-2476
[24] Sun, W. Y., O. M. Sun. Bernoulli Equation and Flow over a Mountain. Geoscience Letters, 2015, 2: 7. DOI: https://doi.org/10.1186/s40562-015-0024-1
[25] Sun, W. Y. Instability in Leapfrog and Forward-Backward Schemes: Part II: Numerical Simulation of Dam Break. J. Computers and Fluids, , 2011, 45: 70- 76.
Downloads
How to Cite
Sun, W.-Y. (2021). Coordinates over Complex Terrain in Atmospheric Model. Journal of Atmospheric Science Research, 4(1), 39–49. https://doi.org/10.30564/jasr.v4i1.2704
Issue
Article Type
Article
License
Copyright © 2021 Author(s)
This is an open access article under the Creative Commons Attribution-NonCommercial 4.0 International (CC BY-NC 4.0) License.
